My researches are mainly focused on implementation of mathematical objects (like Signal Processing filters, controllers, etc.) into embedded digital devices (i.e. into software running into processors or dedicated hardware) with numerical issues (finite precision concerns) in mind.
This topic is at the interface between several domains, such as Signal Processing, Control, Computer Architecture and Computer Arithmetic. In my professional career, I have been successively involved into research teams in these topics.
Since 2009, I am associate Professor in the Computer Science lab (LIP6) of the Pierre and Marie Curie University (Sorbonne Université), working on a “numerical issues in the implementation of embedded computing” theme, with my colleagues and students at the Pequan team (PErformance and QUality of Numerical Algorithms).
In general, my interests are focused on:
-
- numerical implementation of algorithms on embedded targets (software or hardware), mainly for Signal Processing/Control algorithms but not only;
- error analysis of finite precision implementations (mathematical bound on the difference between the mathematical exact object and its finite precision implementation) ;
- optimal implementation problems (find some implementations that minimizes implementation costs, such as power consumption, with constraints on the numerical quality of the implementation).
The main idea is to tackle this problem with a global point of view, combining all the different complementary approaches into a global flow, from mathematical object (such as filters) to code. From a Signal Processing point of view, it consists in modeling all the numerical errors as roundoff noises and uses dedicated tools to evaluate statistically how they propagate up to the output(s). From an Computer Architecture point of view (often linked with the signal processing one), it concerns the Fixed-Point arithmetic, the algorithm-architecture adequacy and, for Hardware cases (FPGAs and ASICs) the optimization of the involved bit-width (in a multiple word-length paradigm). The Control approach shows us how to use the equivalent realization set (a set of mathematically equivalent algorithms, that are no more equivalent in finite precision; it is often parametrized with a free transform matrix, like in the State-Space case), and consider some equivalent algorithms that may requires more operations but are much more well conditioned (or equivalently, that requires less bits to achieve the same final accuracy). And we also intensively used the Computer Arithmetic tools and methods for the error analysis in order to make them reliable (interval arithmetic, reliable computing, rigorous error analysis and multi-precision or arbitrary precision computing). These have been developed mainly for mathematical function implementation, and we try to transpose them to Signal Processing/Control algorithms (the feedback is here a problem key).
Using all this, we are building automatic tools and methodology to transform mathematical objects in an optimal way (with respect to some criteria) into dedicated code, where the bounds on finite precision errors are limited and guaranteed.
As shown in the next figure, several tools/technics (we cannot detailed here) are used and combined to produce reliable code.
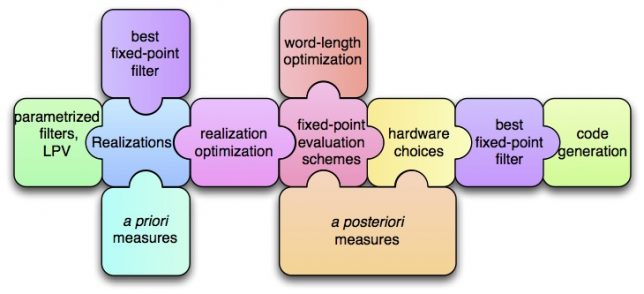
Keywords: finite-precision arithmetic, implementation, error analysis, quantization, fixed-point arithmetic, linear filters
Publications: 9 journals and 35 international conferences (full list here)